Stories
-
![فيديوهات]()
فيديوهات
RT STORIES
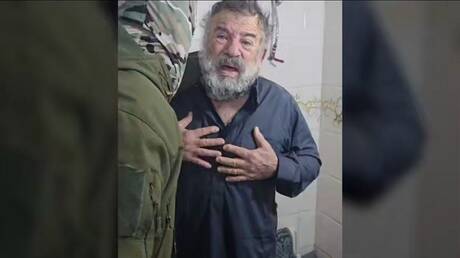
لحظة تحرير المنتج التلفزيوني السوري محمد قبنض.. لقطات حية لحالته المزرية وانفعاله عند التعرّف عليه
![لحظة تحرير المنتج التلفزيوني السوري محمد قبنض.. لقطات حية لحالته المزرية وانفعاله عند التعرّف عليه]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
إسرائيل تعلن وصول 3 مقاتلات F-35 إلى قاعدة "نيفاتيم" الجوية
#اسأل_أكثر #Question_MoreRT STORIES
روسيا.. قلّاب شاحنة يدمر جسرا في مقاطعة روستوف
#اسأل_أكثر #Question_More![فيديوهات]() فيديوهات
فيديوهات
-
![90 دقيقة]()
90 دقيقة
RT STORIES
باعتراف كاراغر.. ليفربول يعاني من مشكلة ومحمد صلاح قد يساعد في الحل
![باعتراف كاراغر.. ليفربول يعاني من مشكلة ومحمد صلاح قد يساعد في الحل]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
صدمة مغربية جديدة بعد خسارة نهائي إفريقيا
![صدمة مغربية جديدة بعد خسارة نهائي إفريقيا]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
قرار دولي يعيد ناشئي روسيا إلى المنافسات العالمية في ثلاث رياضات
![قرار دولي يعيد ناشئي روسيا إلى المنافسات العالمية في ثلاث رياضات]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
ضربة مرفق تنهي مسيرة لاعب وتفتح باب السجن
![ضربة مرفق تنهي مسيرة لاعب وتفتح باب السجن]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
حصاد ذهبي للإمارات في افتتاح موسم بطولات الجوجيتسو 2026
![حصاد ذهبي للإمارات في افتتاح موسم بطولات الجوجيتسو 2026]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_More![90 دقيقة]() 90 دقيقة
90 دقيقة
-
![ترامب والناتو وامتحان غرينلاند]()
ترامب والناتو وامتحان غرينلاند
RT STORIES
ترامب ينشر رسالة من ماكرون دعا فيها لاجتماع مجموعة السبع في باريس بمشاركة روسيا
![ترامب ينشر رسالة من ماكرون دعا فيها لاجتماع مجموعة السبع في باريس بمشاركة روسيا]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
ترامب: الدنمارك عاجزة عن حماية غرينلاند ولن يستطيع أحد حمايتها
![ترامب: الدنمارك عاجزة عن حماية غرينلاند ولن يستطيع أحد حمايتها]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
خبير: ضم ترامب غرينلاند سيشكل كارثة لـ"الناتو"
![خبير: ضم ترامب غرينلاند سيشكل كارثة لـ"الناتو"]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
ميرتس: التعريفات الأمريكية ضد أوروبا ستضر الجانبين
![ميرتس: التعريفات الأمريكية ضد أوروبا ستضر الجانبين]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
الدنمارك تقاطع منتدى دافوس وسط تصاعد الخلاف مع واشنطن حول غرينلاند
![الدنمارك تقاطع منتدى دافوس وسط تصاعد الخلاف مع واشنطن حول غرينلاند]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
التوتر الأوروبي–الأمريكي حول غرينلاند.. ضربات للنفوذ الأمريكي وهزيمة محتملة لمصداقية الناتو
![التوتر الأوروبي–الأمريكي حول غرينلاند.. ضربات للنفوذ الأمريكي وهزيمة محتملة لمصداقية الناتو]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_More![ترامب والناتو وامتحان غرينلاند]() ترامب والناتو وامتحان غرينلاند
ترامب والناتو وامتحان غرينلاند
-
![خطة ترامب لإنهاء الحرب في غزة]()
خطة ترامب لإنهاء الحرب في غزة
RT STORIES
ترامب يهدد ماكرون برسوم طائلة إن لم يقبل الانضمام إلى مجلس السلام في غزة
![ترامب يهدد ماكرون برسوم طائلة إن لم يقبل الانضمام إلى مجلس السلام في غزة]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
ترامب: الرئيس بوتين مدعو لعضوية مجلس السلام في غزة
![ترامب: الرئيس بوتين مدعو لعضوية مجلس السلام في غزة]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
سموتريتش يدعو لإلغاء خطة ترامب ويطالب بفرض السيطرة الكاملة على غزة
![سموتريتش يدعو لإلغاء خطة ترامب ويطالب بفرض السيطرة الكاملة على غزة]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
نتنياهو: لن يكون هناك جنود أتراك أو قطريون داخل قطاع غزة ونحن على أعتاب المرحلة الثانية في خطة ترامب
![نتنياهو: لن يكون هناك جنود أتراك أو قطريون داخل قطاع غزة ونحن على أعتاب المرحلة الثانية في خطة ترامب]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_More![خطة ترامب لإنهاء الحرب في غزة]() خطة ترامب لإنهاء الحرب في غزة
خطة ترامب لإنهاء الحرب في غزة
-
![العملية العسكرية الروسية في أوكرانيا]()
العملية العسكرية الروسية في أوكرانيا
RT STORIES
درونات "أوسا أوكتا" الروسية تضيف لوجستيات جديدة على الجبهة
![درونات "أوسا أوكتا" الروسية تضيف لوجستيات جديدة على الجبهة]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
الدفاع الروسية: تحرير بلدتين شرق وجنوب أوكرانيا
![الدفاع الروسية: تحرير بلدتين شرق وجنوب أوكرانيا]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
خبير أمريكي: واشنطن تسعى لاستعادة العلاقات مع روسيا عبر التسوية الأوكرانية
![خبير أمريكي: واشنطن تسعى لاستعادة العلاقات مع روسيا عبر التسوية الأوكرانية]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_More![العملية العسكرية الروسية في أوكرانيا]() العملية العسكرية الروسية في أوكرانيا
العملية العسكرية الروسية في أوكرانيا
-
![التطورات الميدانية شمال شرق سوريا]()
التطورات الميدانية شمال شرق سوريا
RT STORIES
بيان عربي قوي دعما لسوريا بعد الاتفاق التاريخي
![بيان عربي قوي دعما لسوريا بعد الاتفاق التاريخي]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
قسد: سجن الشدادي الذي يضم آلاف مقاتلي "داعش" خرج عن السيطرة والتحالف الدولي لم يتدخل
![قسد: سجن الشدادي الذي يضم آلاف مقاتلي "داعش" خرج عن السيطرة والتحالف الدولي لم يتدخل]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
الجيش السوري يعلن دخوله مدينة الشدادي بريف الحسكة "بعد إطلاق قسد سراح عناصر من داعش"
![الجيش السوري يعلن دخوله مدينة الشدادي بريف الحسكة "بعد إطلاق قسد سراح عناصر من داعش"]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_MoreRT STORIES
أردوغان: الحكومة السورية نفذت العملية بدقة وسوريا للعرب والتركمان والأكراد والعلويين والسنة والدروز
![أردوغان: الحكومة السورية نفذت العملية بدقة وسوريا للعرب والتركمان والأكراد والعلويين والسنة والدروز]() #اسأل_أكثر #Question_More
#اسأل_أكثر #Question_More![التطورات الميدانية شمال شرق سوريا]() التطورات الميدانية شمال شرق سوريا
التطورات الميدانية شمال شرق سوريا
علماء الرياضيات يكتشفون شكلا جديدا يمكن أن يكسو الجدار دون تكرار!
اكتشف فريق من جامعة أركنساس الشكل الأول الذي يمكنه تغطية الجدار دون إنشاء نمط متكرر.

وتُعرف الخاصية باسم "التبليط غير الدوري"، وحتى الآن لم يتم تحقيقها إلا باستخدام أكثر من شكل واحد.
لكن هذه "القبعة" قادرة على الفتح مع نفسها لإنتاج أنماط ممتدة لانهائية. حتى أنها تحتفظ بقدرتها على التبليط غير الدوري عندما يتغير طول جوانب الشكل الثلاثة عشر، ما يتيح إمكانية وجود المزيد من الأنماط.
ويشير التجانب إلى تغطية سطح مستو بأشكال تتلاءم معا دون أي فجوات أو تداخلات.
ويعرف التبليط غير الدوري بأنه نوع محدد من التبليط حيث لا يكرر نمط الأشكال المستخدمة لتغطية السطح نفسه.
وهذا على عكس التجانب الدوري، والذي يستخدم الأشكال لتغطية السطح بنمط يكرر نفسه بانتظام، مثل المثلثات والمربعات.
وتم اكتشاف المجموعة الأولى من الأشكال التي يمكن أن تخلق أنماطا مختلفة لانهائية معا في عام 1963 من قبل عالم الرياضيات الأمريكي روبرت بيرجر.
ويتألف هذا من 20426 شكلا فريدا، لكن الاكتشاف أدى إلى مزيد من البحث في التبليط غير الدوري، لمعرفة ما إذا كان يمكن خفض هذا الرقم.
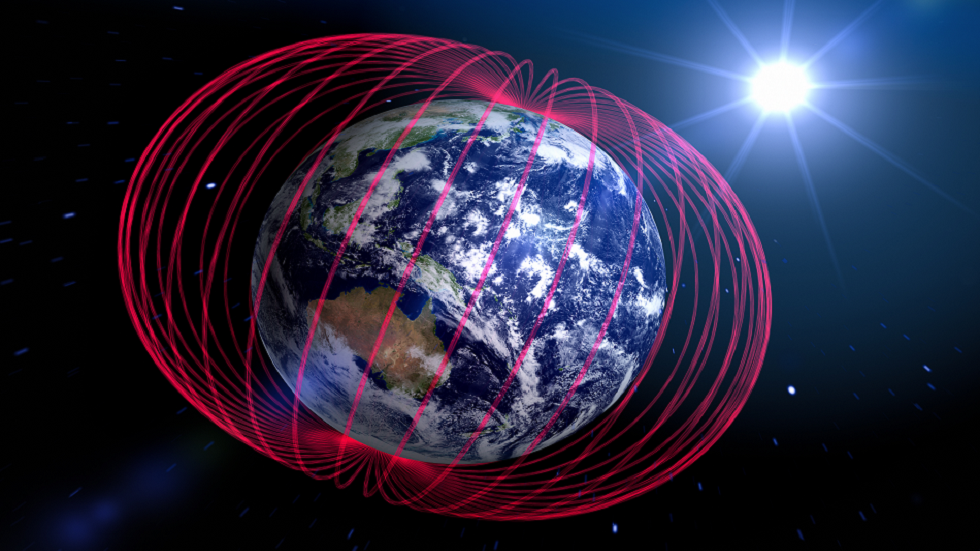
ناسا تتعقب شذوذا ضخما في المجال المغناطيسي للأرض!
وتُعرف مجموعة البلاط غير الدورية الأكثر شهرة باسم "بلاط Penrose''، والتي تتكون من شكلين مختلفين من المعين وتم نشرها لأول مرة في عام 1974.
ومنذ ذلك الحين، كان علماء الرياضيات يبحثون عن "أينشتاين" بعيد المنال. الشكل الذي يمكن أن يحقق تبليط غير دوري من تلقاء نفسه.
وفي دراستهم المؤلفة من 89 صفحة، والتي نُشرت في arXiv، كان الباحثون المقيمون في فايتفيل يهدفون إلى اكتشاف آينشتاين الحقيقي، والذي يعني "حجر واحد" باللغة الألمانية.
وكتبوا: "لطالما كان السؤال مفتوحا حول ما إذا كان هذا البلاط موجودا".
واستخدم الفريق لأول مرة أجهزة الكمبيوتر لغربلة مئات الأشكال المختلفة.
ثم نظروا عن كثب إلى الأشكال التي تم إلقاؤها على أنها آينشتاين محتملة، وحاولوا أن يثبتوا رياضيا أنهم سينتجون تبليط غير دوري.
وقال المعد الرئيسي الدكتور حاييم غودمان شتراوس: "أنت تبحث حرفيا عن شيء واحد في المليون. وتقوم بالتصفية، ثم يكون لديك شيء غريب، ومن ثم يستحق المزيد من الاستكشاف. ثم تبدأ بفحصها يدويا وتحاول فهمها، وتبدأ في سحب الهيكل. وهذا هو المكان الذي سيكون فيه الكمبيوتر عديم القيمة حيث يجب على الإنسان أن يشارك في بناء دليل يمكن للإنسان أن يفهمه".
وكانت "القبعة" الوحيدة التي نجحوا فيها، وقد تمكنوا بالفعل من إثبات عدم دوريتها مرتين.
ويأمل علماء الرياضيات أن تؤدي معرفة شكلها الفريد إلى إنشاء مواد جديدة أكثر قوة، أو لها خصائص مفيدة أخرى.
وغالبا ما تُرى الأنماط المتكررة في الهياكل الجزيئية للمواد البلورية، ما يجعل من السهل كسرها.
المصدر: ديلي ميل


































































































































التعليقات